Probabilities with convolutions

To improve my AI on Leek Wars, I wanted to calculate the probability of several items making a certain sum, namely the enemy's life. Indeed, to maximize the probability of killing, it's sometimes better to use an item 4 times than another 2 times, even if the expectation is the same.

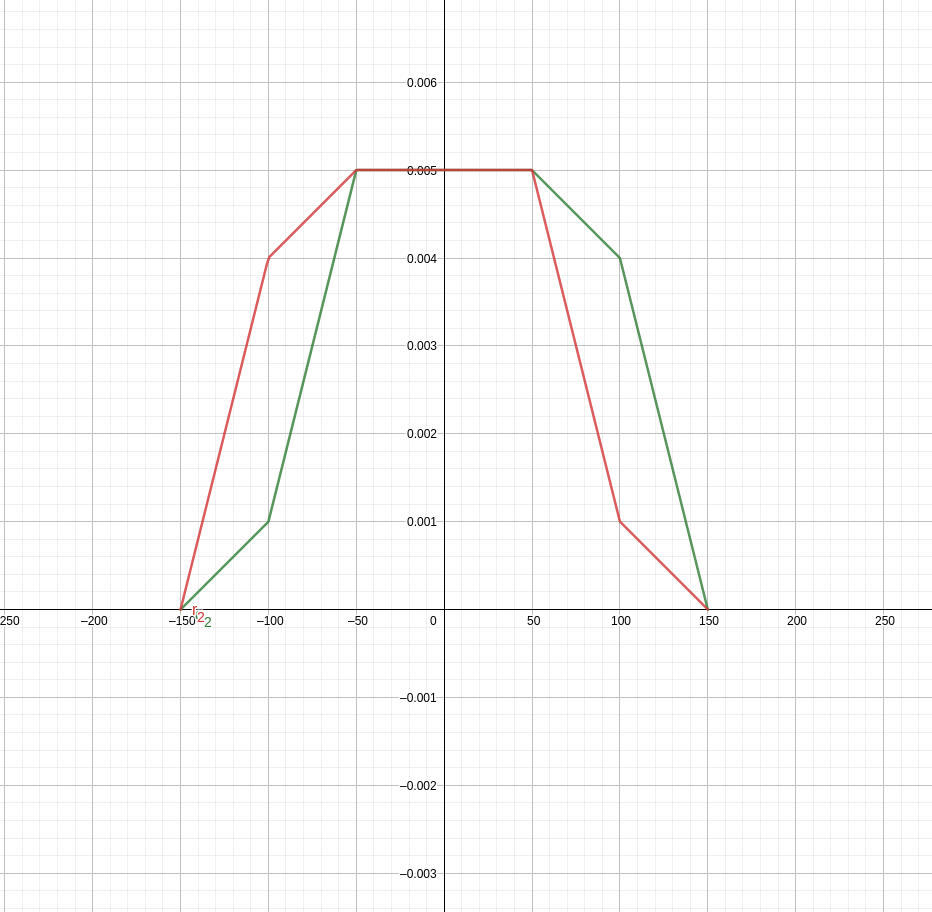
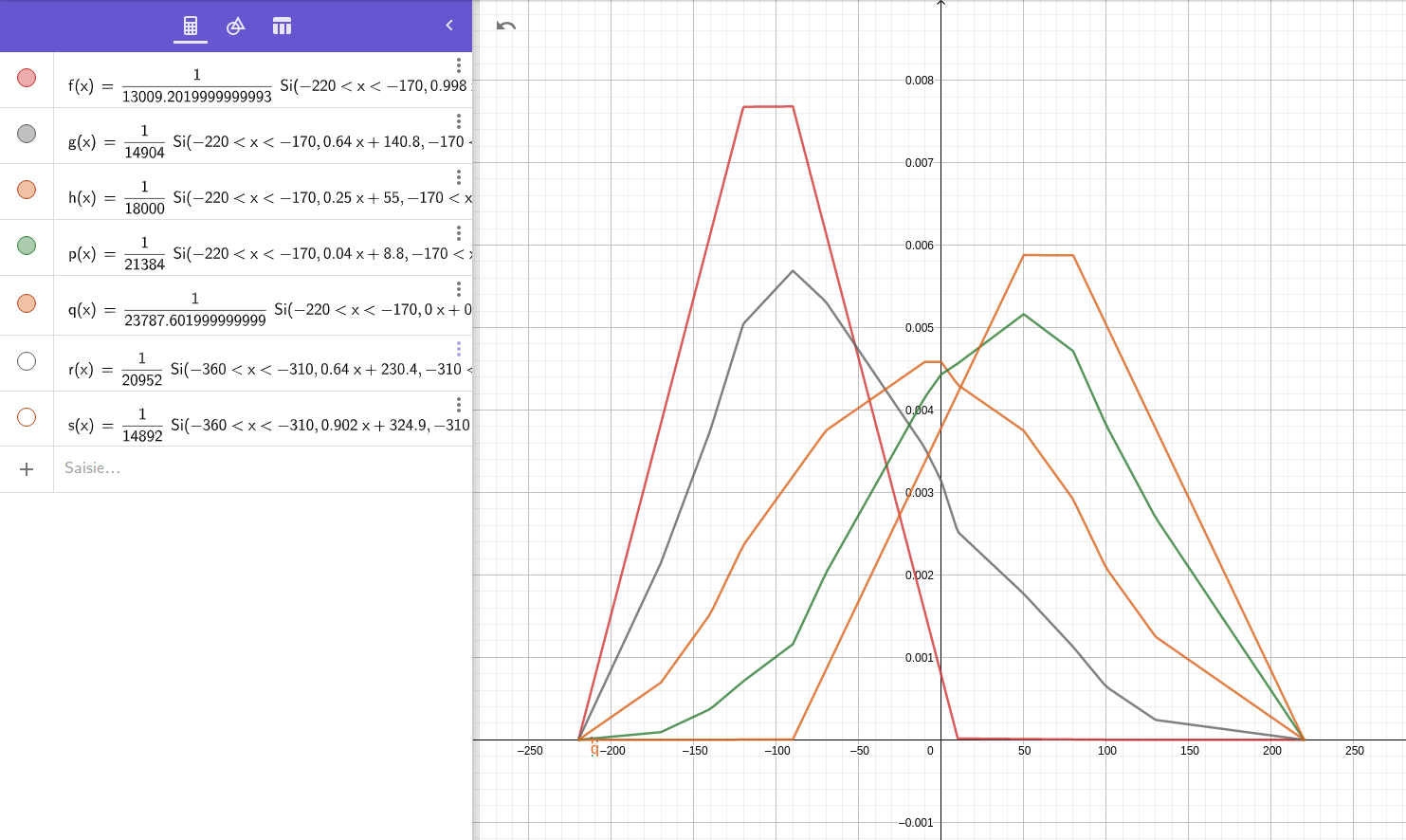
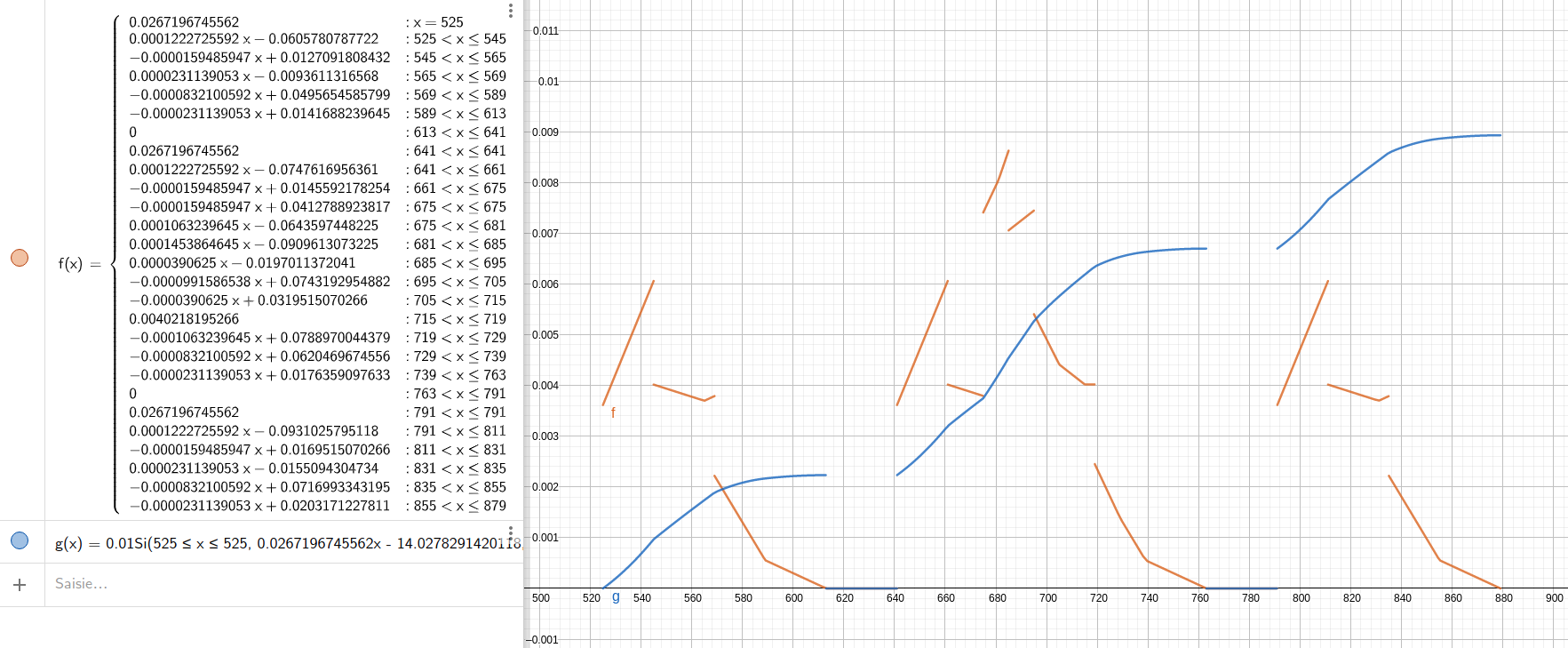
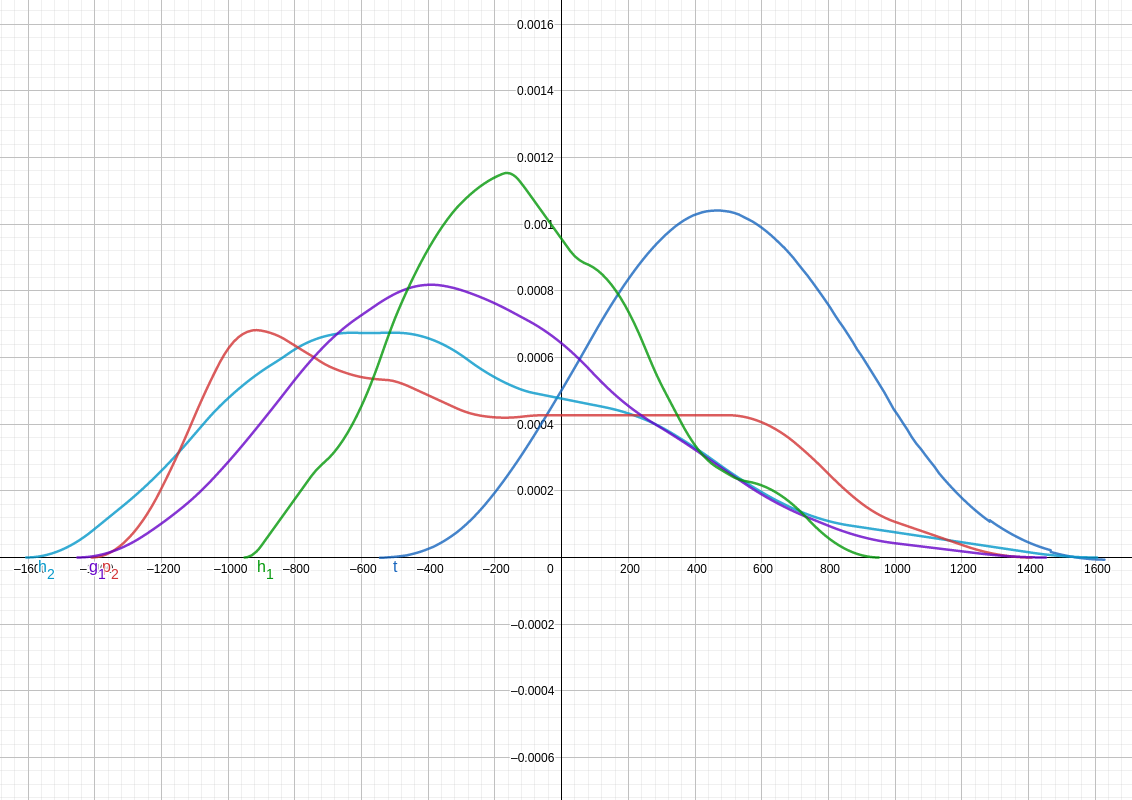
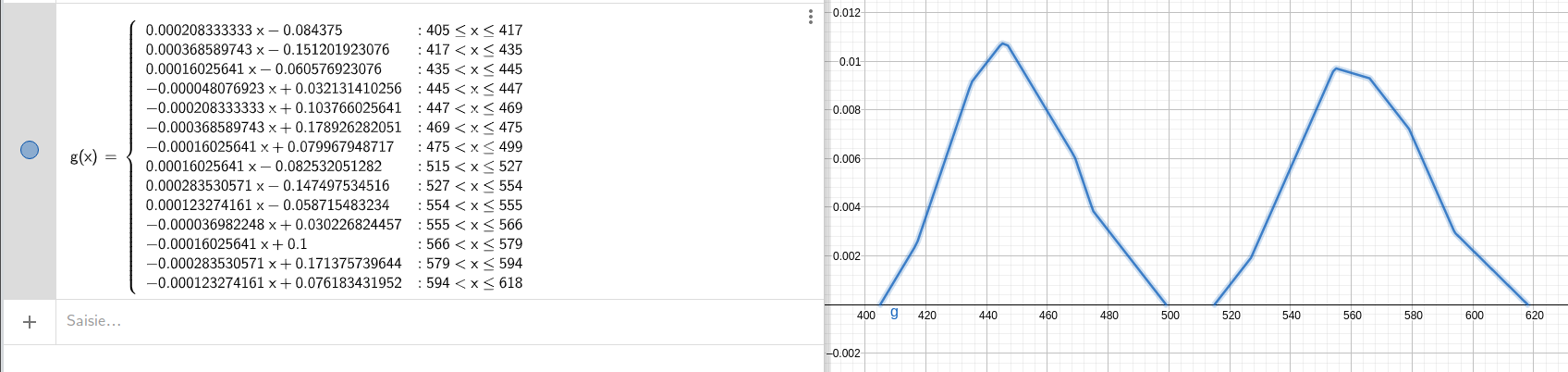
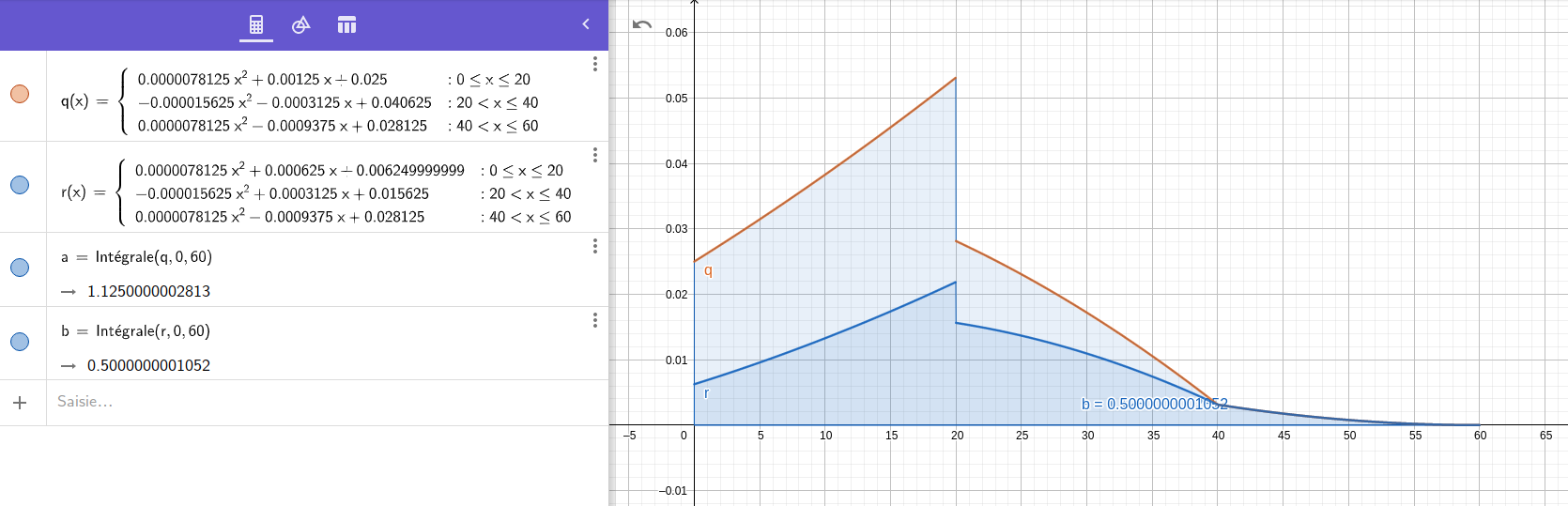
As it happens, the solution was suggested to me by a friend on the game, who pointed me in the direction of convolutions. Indeed, the probability law of the sum of two independent random variables is the convolution product of their respective laws.

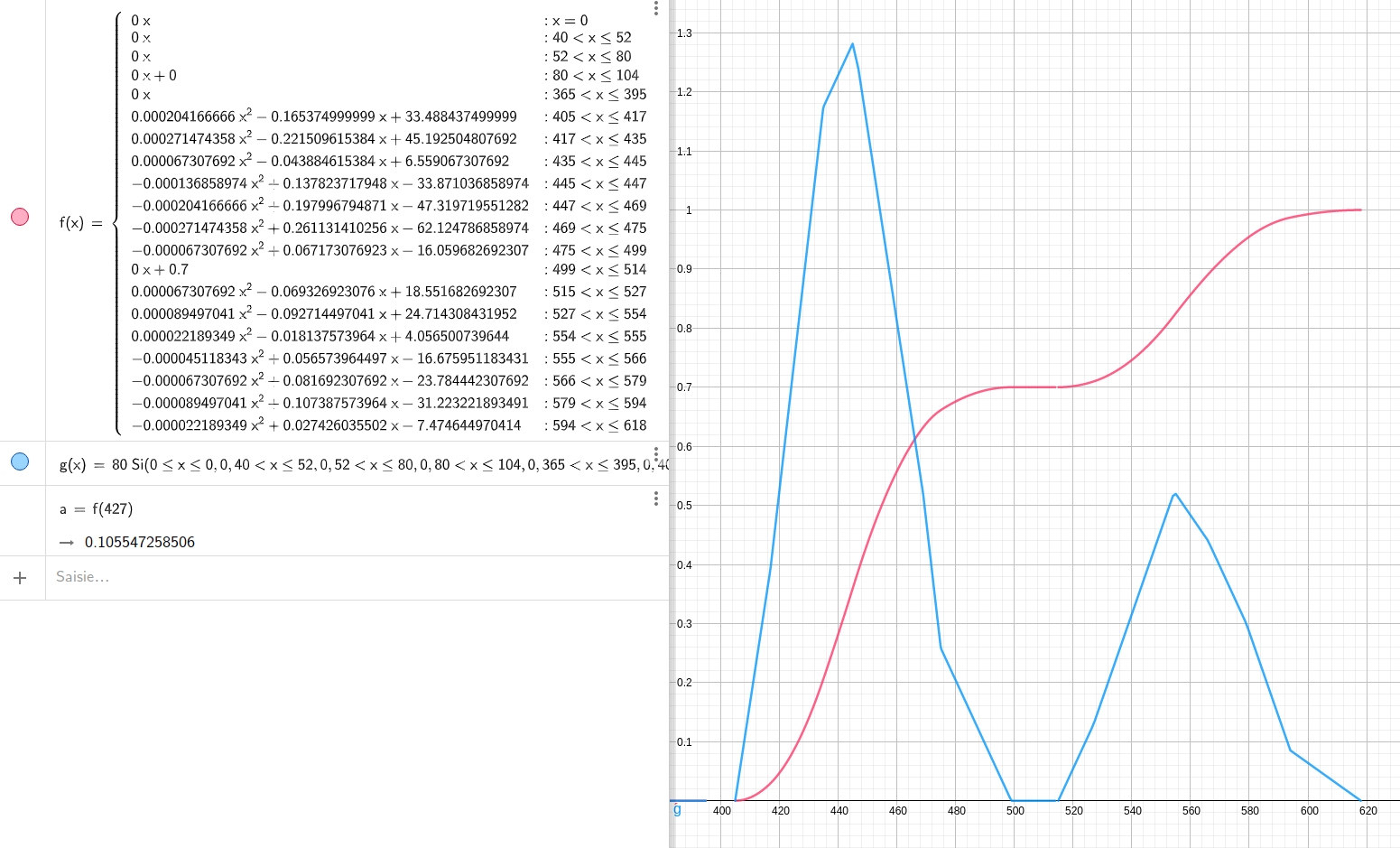
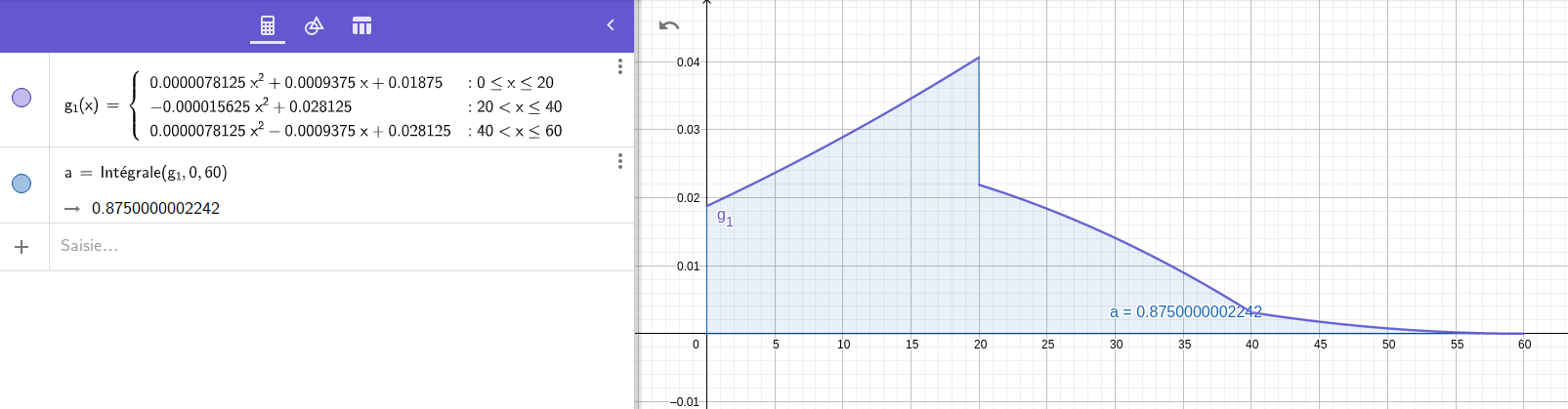
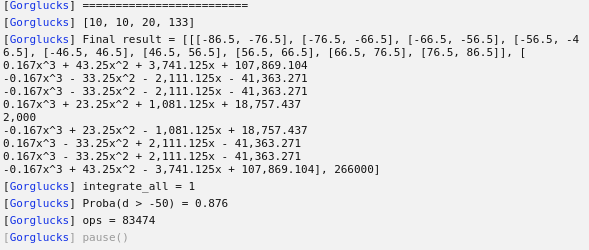
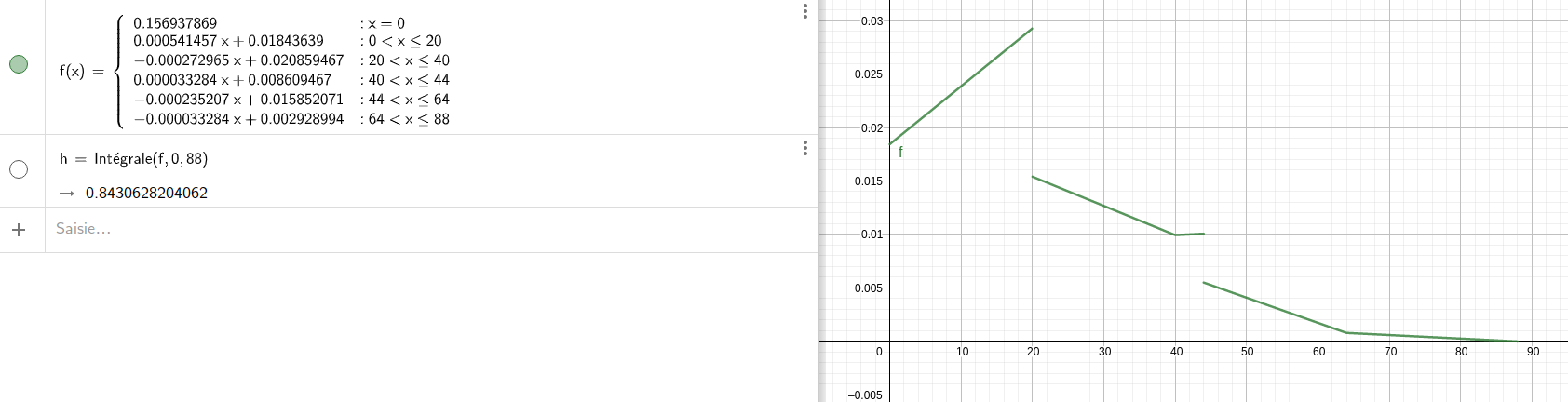
I therefore implemented in LeekScript the calculation of these probability laws of the sum of several items, with the help of Geogebra for visualization. This involves calculating, among other things, the sum and product of two polynomials, the integral of a polynomial, the evaluation of a polynomial into a value, performing an offset by a change of variable (x → x + offset), in order to arrive at the convolution of functions defined by parts.

The algorithm can handle N items and also their critical hits (X% chance of doing more damage), making the final result even more complex.